PROVA DE MATEMÁTICA

As questões de Matemática do Vestibular Unicamp, tanto na primeira quanto na segunda fase, procuram identificar nos candidatos um conhecimento crítico e integrado da Matemática do ensino fundamental e do ensino médio. A leitura atenta dos enunciados das questões, a formulação correta dos problemas matemáticos associados, a elaboração cuidadosa dos cálculos, o uso correto das unidades, a escolha da resposta correta ou a apresentação de respostas claras são procedimentos mínimos e indispensáveis para que o candidato seja bem sucedido. O candidato deve estar familiarizado com a nomenclatura e os símbolos matemáticos usuais. Exige-se do candidato que saiba resolver problemas matemáticos relacionados ao seu cotidiano, bem como interpretar e elaborar tabelas e gráficos, além de responder a questões que tratam de forma mais abstrata o conhecimento matemático. Em geral, as questões não exigem a repetição de demonstrações de teoremas clássicos, embora o conhecimento das definições e a compreensão dos principais teoremas sejam de fundamental importância para um bom desempenho do candidato.

Programa

Conjuntos numéricos
• Representação de conjuntos, subconjuntos, união e interseção de conjuntos
• Números naturais e inteiros: operações fundamentais
• Números primos, fatoração, número de divisores, máximo divisor comum e mínimo múltiplo comum
• Sistema de numeração na base 10 e em outras bases
• Números reais (racionais e irracionais): operações, módulo, desigualdades, representação decimal
• Sequências numéricas, progressões aritmética e geométrica
• Números complexos: operações, módulo, representação geométrica

Funções e gráficos
• A função linear ou afim y = ax + b e seu gráfico
• A função quadrática e seu gráfico

• As funções 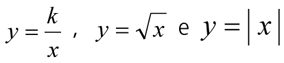e seus gráficos

• Equações e inequações envolvendo funções
• Translação e reflexão de funções, composição de funções
• Função inversa

Polinômios com coeficientes reais
• Operações com polinômios
• Raízes reais e complexas de equações polinomiais
• Fatoração e multiplicidade de raízes, teorema fundamental da álgebra
• Relações de Girard

Contagem e probabilidade
• Princípios de contagem: inclusão-exclusão e multiplicativo
• Arranjos, combinações e permutações
• Espaço amostral e o conceito de probabilidade
• Probabilidade da união e da interseção de eventos
• Probabilidade condicional
• Binômio de Newton e suas aplicações

Sistemas lineares
• Matrizes e suas operações básicas (adição, multiplicação por escalar, transposição, produto)
• Inversa de uma matriz
• Determinante de uma matriz
• Resolução e discussão de sistemas lineares, representação matricial, escalonamento

Geometria plana
• Congruência de figuras geométricas
• Congruência de triângulos
• Paralelas e transversais, teorema de Tales
• Semelhança de triângulos
• Triângulos retângulos, teorema de Pitágoras
• Relações métricas nos triângulos
• Quadriláteros notáveis
• Polígonos regulares, circunferências e círculos, perímetro, área Inscrição e circunscrição

Geometria espacial
• Paralelismo e perpendicularidade entre retas e planos
• Poliedros, prismas e pirâmides, áreas e volumes, troncos
• Cilindros, cones e esferas, áreas e volumes, troncos Inscrição e circunscrição de sólidos

Trigonometria
• Medidas de ângulos, graus e radianos
• Funções trigonométricas e seus gráficos, arcos notáveis
• Identidades trigonométricas fundamentais
• Transformações trigonométricas
• Equações e inequações trigonométricas
• Lei dos senos e lei dos cossenos

Geometria analítica
• Coordenadas no plano
• Distância entre dois pontos do plano, alinhamento de três pontos
• Equação da reta no plano
• Interseções de retas no plano, paralelismo e perpendicularismo, ângulo entre duas retas
• Distância de um ponto a uma reta do plano e área de um triângulo
• Equação da circunferência, determinação de circunferências
• Reta e circunferência: posição relativa
• Elipse, hipérbole e parábola e seus gráficos

Logaritmos e exponenciais
• Potências: definição e propriedades
• A função exponencial e seu gráfico
• Logaritmos: definição e propriedades
• A função logarítmica e seu gráficos
• Equações e inequações logarítmicas e exponenciais